How to prove the addition rule for unions
In my lecture yesterday afternoon we were dealing the axiomatic approach to probability. That is, we start solely from the three axioms of probability, and use those rules to prove various properties. I was explaining to my students that usually the way to solve such problems is to look for a way to write things as disjoint unions – because once you have a disjoint union, you can use the third and most powerful axiom, which says that if $A_1, A_2, \dots$ is a finite or countably infinite sequence of disjoint events, then
\[\mathbb P(A_1 \cup A_2 \cup \cdots) = \mathbb P(A_1) + \mathbb P(A_2) + \cdots .\]In particular, this means that if two events $A$ and $B$ are disjoint, then we have
\[\mathbb P(A \cup B) = \mathbb P(A) + \mathbb P(B) .\]But what if $A$ and $B$ are not disjoint? Then we have the addition rule for unions:
\[\mathbb P(A \cup B) = \mathbb P(A) + \mathbb P(B) - \mathbb P(A \cap B).\]I pointed out to my students that when they saw this result at school they probably said “Well, $\mathbb P(A \cup B)$ is $\mathbb P(A)$ and $\mathbb P(B)$ together, but we’ve counted the overlap twice, so we have to subtract it” – but that’s not a formal proof based just on the three axioms. So what is a formal proof?
Here’s two proofs. This is not a difficult result to prove, and these two proofs are basically the same, really, but they’re presentationally a bit different.
Proof 1
PROOF 1. The problem is that $A \cup B$ is not a disjoint union, so we can’t use Axiom 3 on it. But we can have $A \cup B = A \cup {\text{something}}$ as a disjoint union – and that something must be $B \cap A^{\mathsf c}$, the bit of $B$ that doesn’t overlap with $A$.

So applying Axiom 3 to the disjoint union on the right-hand side of
\[A \cup B = A \cup (B \cap A^{\mathsf c})\]gives
\[\mathbb P(A \cup B) = \mathbb P(A) + \mathbb P(B \cap A^{\mathsf c}) . \tag{1.1}\]But that $\mathbb P(B \cap A^{\mathsf c})$ doesn’t appear in the theorem, so we’ll need to find a different disjoint union containing that, to let us eliminate it. The only real choice is
\[(B \cap A^{\mathsf c}) \cup (A \cap B) = B .\]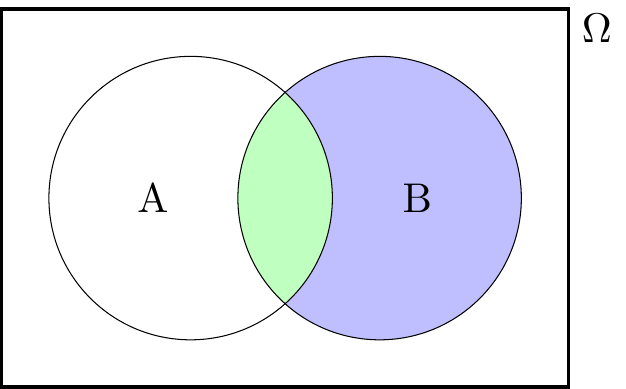
Applying Axiom 3 gives
\[\mathbb P(B \cap A^{\mathsf c}) + \mathbb P(A \cap B) = \mathbb P(B) ,\]rearranging gives
\[\mathbb P(B \cap A^{\mathsf c}) = \mathbb P(B) - \mathbb P(A \cap B) , \tag{1.2}\]and substituting $(1.2)$ into $(1.1)$ gives the result. QED.
Proof 2
PROOF 2. Our problem is that $A$ and $B$ are not disjoint sets, so we can’t apply Axiom 3. Instead lets split everything up into the three disjoint bits $A \cap B^\mathsf{c}$, $A \cap B$ and $B \cap A^{\mathsf c}$.
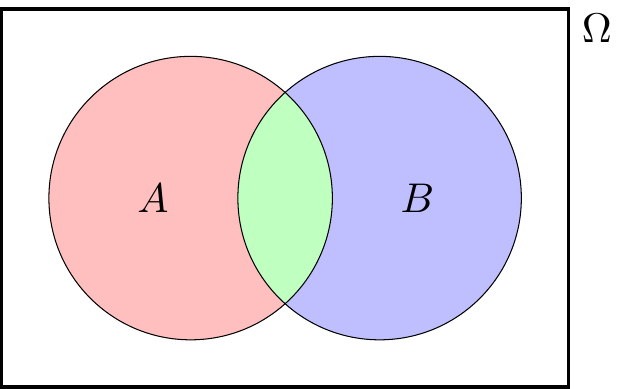
In terms of these three disjoint bits, we now have
\[\begin{align} A &= (A \cap B^\mathsf{c}) \cup (A \cap B) \\ B &= (B \cap A^\mathsf{c}) \cup (A \cap B) \\ A \cup B &= (A \cap B^\mathsf{c}) \cup (B \cap A^\mathsf{c}) \cup (A \cap B), \end{align}\]with all the unions on the right-hand side being disjoint. Applying Axiom 3 to them all gives
\[\begin{align} \mathbb P(A) &= \mathbb P(A \cap B^\mathsf{c}) + \mathbb P(A \cap B) \tag{2.1} \\ \mathbb P(B) &= \mathbb P(B \cap A^\mathsf{c}) + \mathbb P(A \cap B) \tag{2.2} \\ \mathbb P(A \cup B) &= \mathbb P(A \cap B^\mathsf{c}) + \mathbb P(B \cap A^\mathsf{c}) + \mathbb P(A \cap B) . \tag{2.3} \end{align}\]At this stage there are a few slightly different – and I mean very slightly different – ways of finishing this off.
Sub-proof 2a. Here, $(2.3)$ is getting close to the result, but we don’t want the awkward $\mathbb P(A \cap B^\mathsf{c})$ and $\mathbb P(B \cap A^\mathsf{c})$ terms. Rearranging $(2.1)$ and $(2.2)$ gives
\[\begin{align} \mathbb P(A \cap B^\mathsf{c}) &= \mathbb P(A) - \mathbb P(A \cap B) \\ \mathbb P(B \cap A^\mathsf{c}) &= \mathbb P(B) - \mathbb P(A \cap B) , \end{align}\]and substituting these into $(2.3)$ gives the result. QED.
Sub-proof 2b. From $(2.1)$ and $(2.2)$, we have
\[\begin{align} \mathbb P(A) + \mathbb P(B) &= \mathbb P(A \cap B^\mathsf{c}) + \mathbb P(A \cap B) + \mathbb P(B \cap A^\mathsf{c}) + \mathbb P(A \cap B) \\ &= \mathbb P(A \cup B) + \mathbb P(A \cap B) , \end{align}\]where the second equality is by $(2.3)$. Rearranging gives the result. QED.
Sub-proof 2c. By substituting in $(2.1)$ and $(2.2)$, the right-hand side of the desired result is
\[\begin{align} &\mathbb P(A) + \mathbb P(B) - \mathbb P(A \cap B) \\ &\qquad\qquad = \mathbb P(A \cap B^\mathsf{c}) + \mathbb P(A \cap B) + \mathbb P(B \cap A^\mathsf{c}) + \mathbb P(A \cap B) - \mathbb P(A \cap B) \\ &\qquad\qquad = \mathbb P(A \cap B^\mathsf{c}) + \mathbb P(B \cap A^\mathsf{c}) + \mathbb P(A \cap B) , \end{align}\]which, by $(2.3)$, is indeed $\mathbb P(A \cup B)$. QED.
Which is best?
Looking through some textbooks and lecture notes I have been consulting when writing my notes, I see that:
- Grimmett and Walsh’s book uses Proof 2b.
- A discussion after the main proof in Ross’s book uses Proof 2a.
- Blitzstein and Hwang’s book, Scheaffer and Young’s book, Stirzaker’s book, the main proof in Ross’s book, Oliver Johnson’s lecture notes, Richard Weber’s lecture notes, the lecture notes of the previous lecturer of my course, the lecture notes of the previous-but-one lecturer of my course, and me last year all use Proof 1.
So it seems that Proof 1 is the most popular. But I like Proof 2 better. First, Proof 1 uses two steps in an awkward way – splitting $A\cup B$ into two disjoint sets, then later splitting up $B$ – whereas Proof 1 just has one stage of splitting the Venn diagram into three pieces in an obvious way. Second, since the theorem is symmetric in $A$ and $B$, it feels aesthetically as if the proof should be symmetric in $A$ and $B$ too; Proof 2 is, but Proof 1 (which started by picking $A$ as the bigger half of the $A \cup B$ split) is not. Finally, I think Proof 2 is just simpler to remember – this is the main reason I changed for my lectures this year. (I’m trying to lecture the whole thing without notes, so am keen to keep things simple wherever I can.)
But, then, which of the sub-proof finishes are best? In my lectures, I used Sub-proof 2a, because I didn’t have time then to consider alternatives and it seemed the most “obvious” way to finish, requiring the least thinking. Sub-proof 2c is perhaps the slickest, but it “uses the answer” in a slightly unsatisfying way. (How do you know to look at $\mathbb P(A) + \mathbb P(B) - \mathbb P(A \cap B)$? Because the result of the theorem says so!) Proof 2b is appealing because it seems the closest to the “you add up $\mathbb P(A)$ and $\mathbb P(B)$ but have accidentally counted the overlap twice” informal argument, although I’m less sure I could convince my students that looking at $\mathbb P(A) + \mathbb P(B)$ is the “obvious” thing to do than Sub-proof 2a. So I think the jury remains out on that.