Problem sheet 4

You should attempt all these questions and write up your solutions in advance of your workshop in week 5 (Monday 22 or Tuesday 23 February) where the answers will be discussed.

1. Consider the Markov chain with state space \(\mathcal S = \{1,2,3,4\}\) and transition matrix \[ \mathsf P = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 1-\alpha & 0 & \alpha & 0 \\ 0 & \beta & 0 & 1-\beta \\ 0 & 0 & 0 & 1 \end{pmatrix} \] where \(0 < \alpha, \beta < 1\).

(a) Draw a transition diagram for this Markov chain.

Solution.

Figure 8.1: Transition diagram for Question 1.

(b) What are the communicating classes for this Markov chain? Is the chain irreducible? Which classes are closed? Which states are absorbing?

Solution. Clearly \(\{1\}\) and \(\{4\}\) are closed communicating classes, so \(1\) and \(4\) are absorbing states. The other class, \(\{2,3\}\) is not closed. Because there are multiple classes, the chain is not irreducible.

(c) Find the hitting probability \(h_{21}\) that, starting from state 2, the chain hits state 1.

Solution. It’s clear that \(h_{11} = 1\) and \(h_{41} = 0\). Then, by conditioning on the first step, we have \[\begin{gather*} h_{21} = \alpha h_{31} + (1-\alpha) h_{11} = \alpha h_{31} + 1 - \alpha \\ h_{31} = \beta h_{21} + (1-\beta) h_{41} = \beta h_{21} . \end{gather*}\] Substituting the second equation into the first, we get \(h_{21} = \alpha\beta h_{21} + 1 - \alpha\), so \[ h_{21} = \frac{1-\alpha}{1-\alpha\beta} . \]

(d) What is the expected time, starting from state 2, to reach an absorbing state?

Solution. Let’s write \(A = \{1,4\}\) for the absorbing states, and \(\eta_{iA}\) for the time to reach an absorbing state starting from state \(i\). Clearly \(\eta_{1A} = \eta_{4A} = 0\). By conditioning on the first step, we have \[\begin{gather*} \eta_{2A} = 1 + \alpha \eta_{3A} + (1-\alpha) \eta_{1A} = 1 + \alpha \eta_{3A} \\ \eta_{3A} = 1 + \beta \eta_{2A} + (1-\beta) \eta_{4A} = 1+\beta \eta_{2A} . \end{gather*}\] Substituting the second equation into the first gives \(\eta_{2A}= 1 + \alpha + \alpha\beta \eta_{2A}\), so \[ \eta_{2A} = \frac{1+\alpha}{1-\alpha\beta} . \]

2. Consider the Markov chain with state space \(\mathcal S = \{1,2,3,4,5\}\) and transition matrix \[ \mathsf P = \begin{pmatrix} 0 & \frac13 & \frac23 & 0 & 0 \\ 0 & 0 & 0 & \frac14 & \frac34 \\ 0 & 0 & 0 & \frac14 & \frac34 \\ 1 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 \end{pmatrix} . \]

(a) Draw a transition diagram for this Markov chain.

Solution.

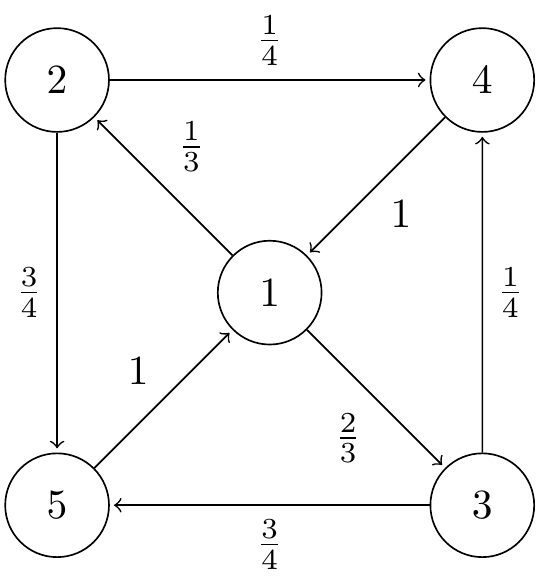
Figure 8.2: Transition diagram for Question 2.

(b) Show that the chain is irreducible.

Solution. We have paths \(1 \to 2 \to 4 \to 1\) and \(1 \to 3 \to 5 \to 1\), so every state communicates with state 1, and by transitivity every state communicates with every other state.

(c) What are the periods of the states?

Solution. Any path from \(1\) to \(1\) goes \(1 \to \{2 \text{ or }3\} \to \{4 \text{ or }5\} \to 1\). So \(p_{11}^{(n)} > 0\) if and only if \(n\) is a multiple of \(3\). So state \(1\) has period \(d_1 = 3\). Because the chain is irreducible, all other states have period \(3\) too.

(d) Find the expected hitting times \(\eta_{i1}\) from each state \(i\) to 1, and the expected return time \(\mu_i\) to 1.

Solution. We could do this through a traditional conditioning on the first step argument. But in fact, the cyclic structure \(1 \to \{2 \text{ or }3\} \to \{4 \text{ or }5\} \to 1\) makes it immediately clear that \(\eta_11 = 0\), \(\eta_{41}=\eta_{51} = 1\), \(\eta_{21} = \eta_{31} = 2\), and \(\mu_1 = 3\).

3.

(a) Show that every Markov chain on a finite state space \(\mathcal S\) has at least one closed communicating class.

Solution. For communicating classes \(C,D\), let’s write \(C \to D\) if there is an \(i \in C\) and \(j \in D\) with \(i \to j\). Note that we can’t have both \(C \to D\) and \(D \to C\) if \(C\) and \(D\) are distinct classes. This is because there would be \(i_1, j_2 \in C\) and \(j_1, i_2 \in D\) such that \(i_1 \to j_1 \to i_2 \to j_2 \to i_1\), so they would be the same class. Let’s also note that there are a finite number of classes \(m\).

Pick a class \(C_1\). If \(C_1\) is closed, we are done; otherwise \(C_1 \to C_2\) for some other class \(C_2\). If \(C_2\) is closed, we are done; otherwise \(C_2 \to C_3\) for some class \(C_3\) different to \(C_1\) and \(C_2\). (It can’t be \(C_1\) by the argument above.) We repeat: if \(C_k\) is closed, we are done; otherwise there’s a new class \(C_{k+1}\) with \(C_k \to C_{k+1}\). We eventually find a closed class: we either terminate before step \(m\) at a closed class, or otherwise \(C_m\) must be closed, as none of the previous \(m-1\) classes can be accessible from it, by our earlier argument.

(b) Give an example of a Markov chain that has no closed communicating classes.

Solution. By part (a), the state space must be infinite. Here’s one example: take \(\mathcal S = \mathbb Z\), and \(X_{n+1} = X_n + 1\) with probability 1, so the Markov chain just marches up and up. There are no states \(i\) and \(j\) such that \(i \leftrightarrow j\) (except for states communicating with themselves) so each state is a separate class. But clearly there is no absorbing state.

4. Prove or give a counterexample: The period of a state \(i\) is the smallest \(d > 0\) such that \(p_{ii}(d) > 0\).

Solution. The statement is not true. Here’s one counterexample:

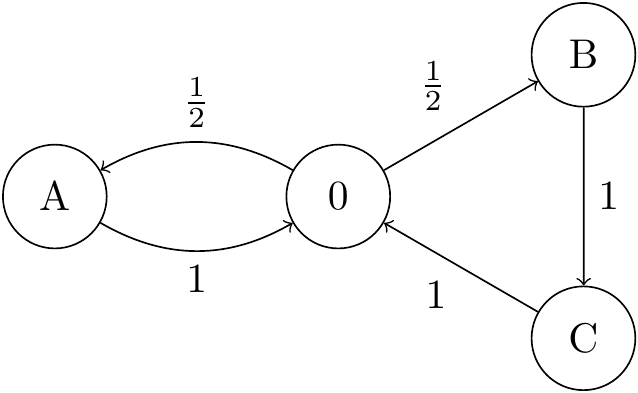
Figure 8.3: Transition diagram for a counterexample for Question 4.

We see that \(p_{00} = p_{00}(1) = 0\), but \(p_{00}(2) = \frac12 > 0\) (going via A) and \(p_{00}(3) = \frac12 > 0\) (going via B and C). Hence \(d_0 \leq \text{gcd}\{2,3\} = 1\), so \(d_0 = 1\), contradicting the statement in the question.

5. Consider the simple random walk with \(p < \frac12\), and let \(i > 0\). Show that \(\eta_{i0} = i/(q-p)\).

Solution. By conditioning on the first step, we have \[ \eta_{i0} = 1 + p\eta_{i+1\,0} + q\eta_{i-1\,0} . \] Either by solving this linear difference equation directly or by remembering the solution from when we did expected duration of the gambler’s ruin, the general solution is \[ \eta_{i0} = A + B\rho^i + \frac{i}{q-p} , \] where \(\rho = q/p > 0\).

We have one initial condition \(\eta_{00} = 0\) (since we’re “already there”). This gives \(0 = A + B\), so we have \[ \eta_{i0} = -B + B\rho^i + \frac{i}{q-p} = B(\rho^i - 1) + \frac{i}{q-p} . \]

We now have to use the principle of the minimum non-negative solution. Since \(\rho > 1\), we also have \(\rho^i - 1 > 0\). Hence \(B\) must be non-negative, to ensure the whole solution is non-negative, but we want \(B\) to be as small as possible, to ensure minimality. Hence we must have \(B = 0\), finally giving the solution \[ \eta_{i0} = \frac{i}{q-p} \] as desired.

6. Consider the Markov chain with the following transition matrix and transition diagram:

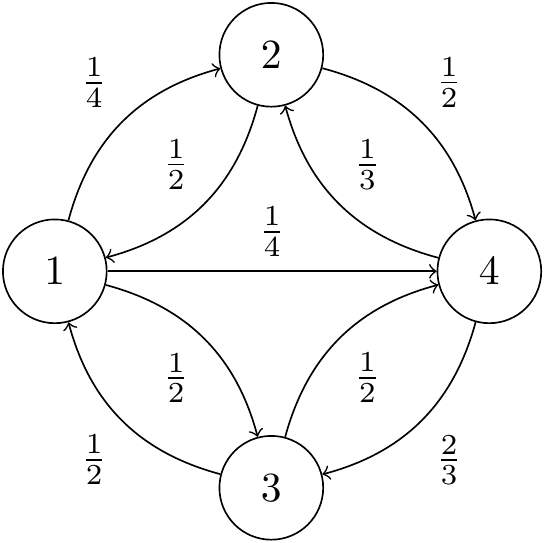
Figure 8.4: Transition diagram for Question 6.

\[ \mathsf P = \begin{pmatrix} 0 & \frac14 & \frac12 & \frac14 \\ \frac12 & 0& 0& \frac12 \\ \frac12 & 0& 0& \frac12 \\ 0 & \frac13 & \frac23 & 0 \end{pmatrix} \]

The Markov chain starts from state 1.

(a) What is the probability that we hit state 2 before we hit state 3?

Solution. Write \(k_i\) for the probability we hit state 2 before state 3 starting from \(i\). Then clearly \(k_2 = 1\) (since we’ve hit 2 first) and \(k_3 = 0\) (since we’ve hit 3 first). Further, by conditioning on the first step, \(k_4 = \frac13 k_2 + \frac23 k_3 = \frac13\), and \[ k_1 = \tfrac14 k_2 + \tfrac12k_3 + \tfrac14 k_4 = \tfrac14 + \tfrac14 k_4 = \tfrac14 + \tfrac14\tfrac13 = \tfrac13 . \] The desired solution is \(k_1 = \frac13\).

(b) What is the expected time until we hit a state in the set \(\{2,3\}\)?

Solution. Let \(A = \{2,3\}\), and \(\eta_{iA}\) be the expected time until hitting the first of states \(2\) and \(3\) starting from \(i\). Clearly \(\eta_{2A} = \eta_{3A} = 0\). By conditioning on the first step, \(\eta_{4A} = 1+ \frac13 \eta_{2A} + \frac23 \eta_{3A} = 1\), and \[ \eta_{1A} = 1 + \tfrac14 \eta_{2A} + \tfrac12\eta_{3A} + \tfrac14 \eta_{4A} = 1 + \tfrac14 = \tfrac54 . \] The desired solution is \(\eta_{1A} = \tfrac54\).