Problem sheet 5

You should attempt all these questions and write up your solutions in advance of your workshop in week 6 (Monday 1 or Tuesday 2 March) where the answers will be discussed.

1. Find a stationary distribution for the Markov chain with transition matrix \[ \mathsf P = \begin{pmatrix} \frac13 & \frac23 & 0 \\ \frac16 & \frac13 & \frac12 \\ 0 & \frac13 & \frac23 \end{pmatrix} . \]

Solution. The equations are \[\begin{align*} \pi_1 &= \tfrac13 \pi_1 + \tfrac16 \pi_2 \\ \pi_2 &= \tfrac23 \pi_1 + \tfrac13 \pi_2 + \tfrac23 \pi_3 \\ \pi_3 &= \phantom{\tfrac23 \pi_1} + \tfrac12 \pi_2 + \tfrac23 \pi_3 \end{align*}\] It’ll make out lives more pleasant if we pick \(\pi_2\) as the working variable and delete the second equation. The first equation becomes \(\pi_1 = \tfrac14 \pi_2\), and the third equation become \(\pi_3 = \tfrac32 \pi_2\). The normalising condition is \[ \pi_1 + \pi_2 + \pi_3 = \left( \tfrac14 + 1 + \tfrac32\right) \pi_2 = \tfrac{11}{4} \pi_2 . \] So \(\pi_2 = \frac4{11}\), so \(\pi_1 = \frac{1}{11}\) and \(\pi_3 = \frac{6}{11}\). The stationary distribution is \(\boldsymbol\pi = (\frac{1}{11}, \frac{4}{11}, \frac{6}{11})\).

2. Consider a Markov chain with state space \(\mathcal S = \{1,2,3,4\}\) and transition matrix \[ \mathsf P = \begin{pmatrix} \frac14 & \frac12 &\frac14 & 0 \\ \frac14 & \frac14 & \frac12 & 0 \\ \frac12 & \frac12 & 0 & 0 \\ \frac14 & 0 &\frac14 & \frac 12 \end{pmatrix} . \]

(a) Draw a transition diagram for this Markov chain.

Solution.

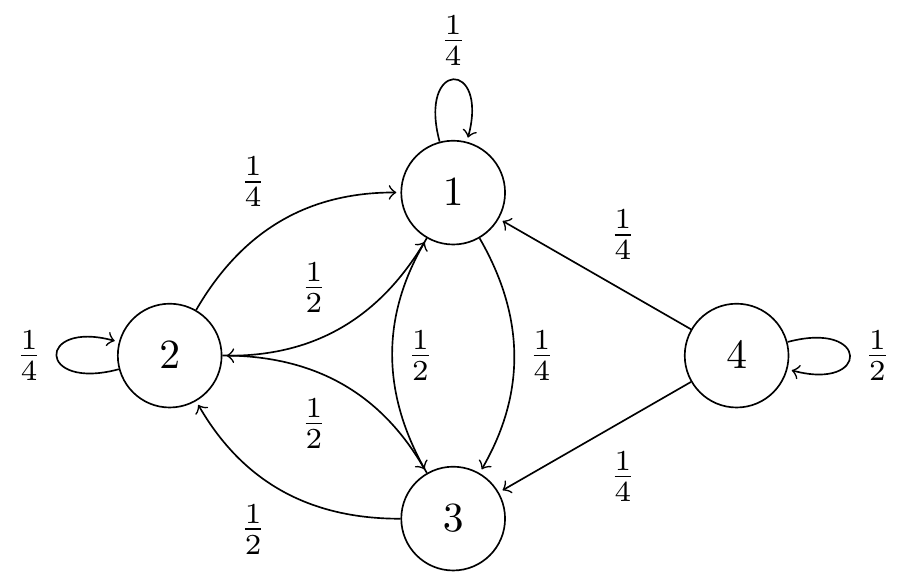
Figure 10.2: Transition diagram for Question 2.

(b) Identify the communicating classes. State whether each class closed or not. State whether each class is positive recurrent, null recurrent, or transient.

Solution. The class \(\{1,2,3\}\) is closed, so is positive recurrent. The class \(\{4\}\) is not closed, so is transient.

(c) Find a stationary distribution for this Markov chain.

Solution. First, we write out the equations \(\boldsymbol\pi = \boldsymbol\pi\mathsf P\), which are \[\begin{align*} \pi_1 &= \tfrac14\pi_1 + \tfrac14\pi_2 + \tfrac12\pi_3 + \tfrac14\pi_4 \\ \pi_2 &= \tfrac12\pi_1 + \tfrac14\pi_2 + \tfrac12\pi_3 \\ \pi_3 &= \tfrac14\pi_1 + \tfrac12\pi_2 \phantom{{}+\tfrac12\pi_3} + \tfrac14\pi_4 \\ \pi_4 &= \phantom{\tfrac12\pi_1 + \tfrac14\pi_2 + \tfrac12\pi_3+{}} \tfrac12 \pi_4 . \end{align*}\] From the fourth equation we immediately see that \(\pi_4 = 0\). Second, we rewrite the first two of the other equations with \(\pi_1\) as the working variable, which gives \[\begin{align} 3\pi_1 &= \phantom{3}\pi_2 + 2\pi_3 \tag{1} \\ 2\pi_1 &= 3\pi_2 - 2\pi_3 \tag{2} . \end{align}\] Adding (1) and (2) gives \(5\pi_1 = 4\pi_2\), so \(\pi_2 = \frac54\pi_1\). Substituting this into (1) and solving gives \(\pi_3 = \frac78 \pi_1\). Third, the normalising condition is \[ \pi_1 + \pi_2 + \pi_3 + \pi_4 = \pi_1 + \tfrac54\pi_1 + \tfrac78\pi_1 + 0 = \tfrac{25}{8}\pi_1 = 1, \] so \(\pi_1 = \frac{8}{25}\). Hence, we have a stationary distribution \[ \boldsymbol\pi = \left(\tfrac{8}{25} \quad \tfrac{10}{25} \quad \tfrac{7}{25} \quad 0 \right) .\]

(d) Is this the only stationary distribution?

Solution. Yes. The Markov chain has one positive recurrent class, so there is a unique stationary distribution, and it is supported only on that class.

3. Consider a Markov chain with state space \(\mathcal S = \{1,2,3,4,5\}\) and transition matrix \[ \mathsf P = \begin{pmatrix} \frac13 & \frac23 & 0 &0 & 0 \\ \frac13 & \frac23 & 0 &0 & 0 \\ 0 &\frac35 & \frac15 & \frac15 & 0 \\ 0 & 0 & 0 & \frac14 &\frac34 \\ 0 & 0 & 0 & \frac12 & \frac12 \end{pmatrix} . \]

(a) Draw a transition diagram for this Markov chain.

Solution.

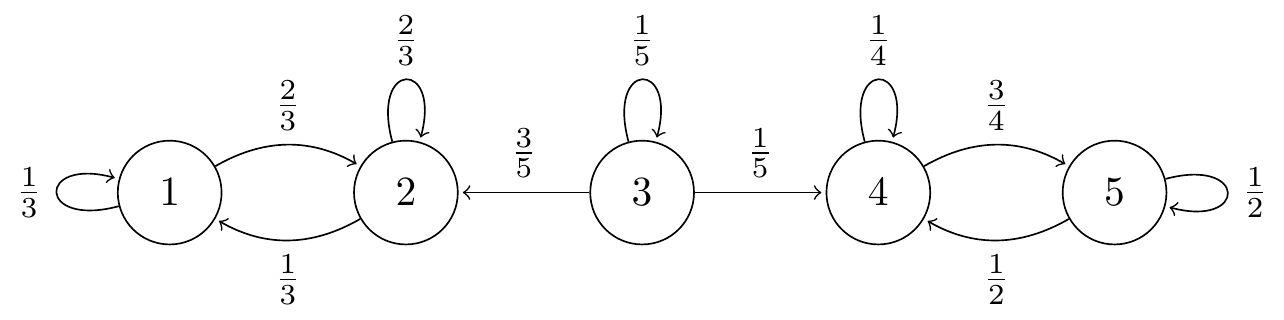
Figure 10.3: Transition diagram for Question 3.

(b) Identify the communicating classes. State whether each class closed or not. State if each class is positive recurrent, null recurrent, or transient.

Solution. The class \(\{1,2\}\) is closed, so is positive recurrent. The class \(\{3\}\) is not closed, so is transient. The class \(\{4,5\}\) is closed, so is positive recurrent.

(c) Find all of the stationary distributions for this Markov chain.

Solution. We can have a stationary distribution supported on either of the positive recurrent classes, but we will always have \(\pi_3 = 0\), as that state is transient. For the class \(\{1,2\}\) we have \[ \pi_1 = \tfrac13\pi_1 + \tfrac13\pi_2 \qquad \pi_2 = \tfrac23\pi_1 + \tfrac23\pi_2 , \] giving \(\pi_2 = 2\pi_1\), and a stationary distribution \((\tfrac 13, \tfrac23, 0, 0, 0)\). For the class \(\{4,5\}\), we have \[ \pi_4 = \tfrac14\pi_4 + \tfrac12\pi_5 \qquad \pi_5 = \tfrac34\pi_4 + \tfrac12\pi_5 , \] giving \(3\pi_4 = 2\pi_5\), and a stationary distribution \((0,0,0,\frac25,\frac35)\). Finally, any linear combination of those where the coefficients are positive and add to \(1\) will also be a stationary distribution, so we have a family of stationary distributions \[ \left( \tfrac13\alpha \quad \tfrac23\alpha \quad 0 \quad \tfrac25(1-\alpha) \quad \tfrac35(1-\alpha) \right) \] for \(0 \leq \alpha \leq 1\).

4. Consider the simple random walk \((X_n)\) on \(\mathcal S = \mathbb Z_+ = \{0,1,2,\dots\}\) with up probability \(p\) and down probability \(q = 1-p\), and a mixed barrier at \(0\), where \(p_{01} = p\), \(p_{00} = q\), and \(p_{0i} = 0\) otherwise. We seek a stationary distribution for this Markov chain.

(a) Suppose \(p \neq \frac12\). Show that the general solution to \[ \pi_j = \sum_i \pi_i p_{ij} = p\pi_{j-1} + q\pi_{j+1} \] is \(\pi_i = A + B\tau^i\), where \(\tau = p/q\).

Solution. Let’s rewrite this as \(q\pi_{j+1} - \pi_j + p\pi_{j-1} = 0\). This is a homogeneous linear difference equation. The characteristic equation is \(p\lambda^2 - \lambda + p = 0\), which factorises as \((q\lambda - p)(\lambda-1) = 0\) (using that \(p + q = 1\)), which has solutions \(\lambda = 1\) and \(\lambda = p/q = \tau\). Since \(p \neq \frac12\), these roots are distinct. So the general solution is \(\pi_i = A + B\tau^i\).

(b) Show that the initial condition \(\pi_0 = q\pi_0 + q\pi_1\) gives \(A = 0\).

Solution. The initial condition gives \[ A + B = q(A + B) + q(A + B\tau) ,\] which after rearranging gives \((1-2q)A = 0\), where we have used \(q + q\tau = q + p = 1\). Since \(1-2q\neq 0\), we must have \(A = 0\).

(c) By considering the normalising condition \(\sum_i \pi_i =1\), work out for what values of \(p \neq \frac12\) there exists a stationary distribution for \((X_n)\). What is the stationary distribution (when it exists)?

Solution. We have \(\pi_i = B\tau^i\), so require \(B \sum_{i=1}^\infty \tau^i = 1\). When \(p > \frac12\), then \(\tau > 1\) and the sum does not converge, and we have no stationary distribution. When \(p < \frac12\), then \(\tau < 1\), so \[ \sum_{i=1}^\infty \tau^i = \frac{1}{1-\tau} \qquad \Rightarrow \qquad B = \frac{1}{\frac{1}{1-\tau}} = 1 - \tau, \] so we have a geometric stationary distribution \(\pi_i = (1-\tau)\tau^i\).

(d) Does there exist a stationary distribution when \(p = \frac12\)?

Solution. Here, the linear difference equation has general solution \(\pi_i = A + Bi\), as we saw with the symmetric gambler’s ruin problem. The initial condition gives \(A = \frac12A + \frac12(A + B)\), and so \(B = 0\), giving \(\pi_i = A\). The normalisation condition is \(\infty \times A = 1\), which cannot be fulfilled. Hence no stationary distribution exists.

5. The infinite rooted binary tree is a graph with no cycles. There is one special vertex, the root 0, that has two edges, and every other edge has three edges. A Markov chain \((X_n)\) starts from 0, then at each time step, takes one of the edges coming out of the current vertex and moves along it to the neighbouring vertex. Note that a step can go away from the root or towards the root.

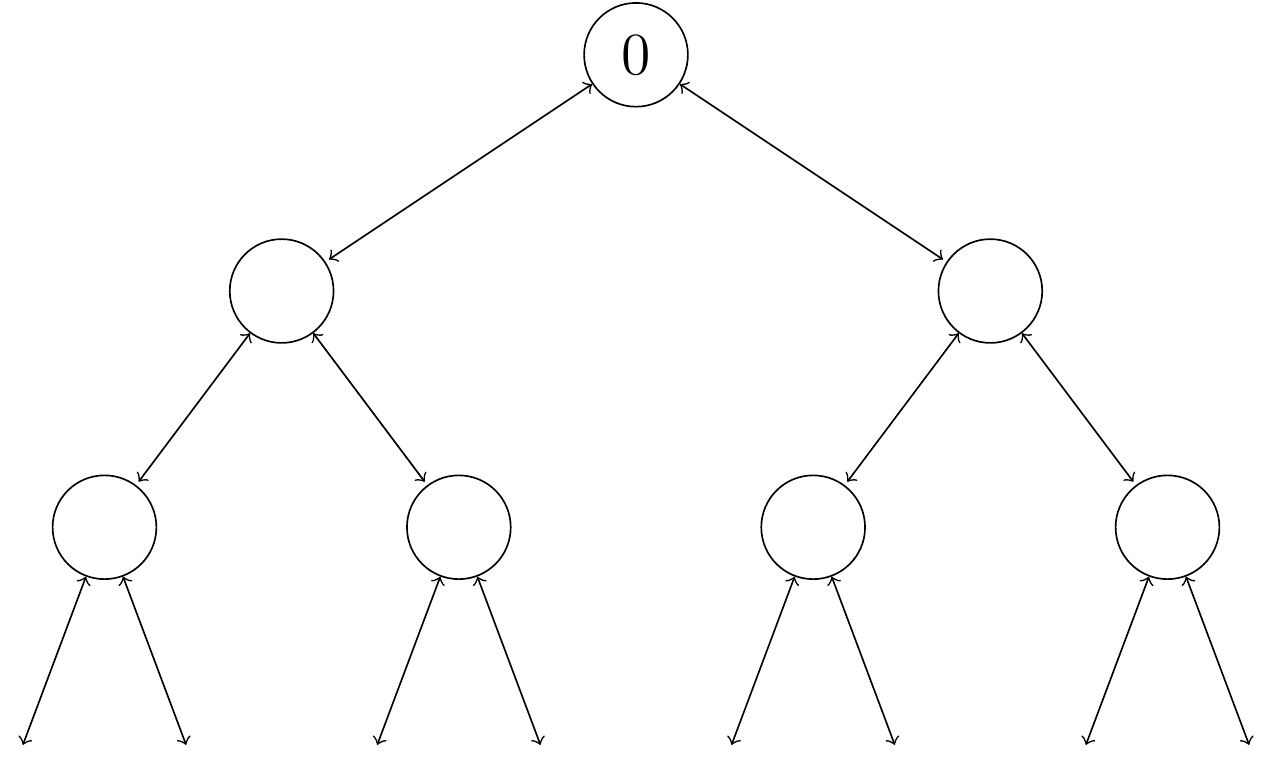
Figure 10.4: The first three-and-a-bit levels of the rooted binary tree.

By considering the distance of \((X_n)\) from the root, or otherwise, show that \((X_n)\) is transient.

Solution. We want to show that \(m_0\), the return probability to the root, is strictly less than 1.

Let \(Y_n\) be the distance of \(X_n\) from the root as suggested in the question. Then \(X_n\) returns to to the root if and only if \(Y_n\) returns to \(0\), so we can look at that instead.

If \((Y_n)\) is the distance from the root, than at each time step \(Y_{n+1} = Y_n + 1\) with probability \(\frac23\), if we take either of the two edges away from root, or \(Y_n = Y_n - 1\) with probability \(\frac13\), if we take the edge back towards the root. If \(Y_n = 0\) is at the root, then \(Y_{n+1} = Y_n+1\). So \((Y_n)\) is a simple random walk with positive drift \(p = \frac23 > \frac12\) and a reflecting barrier at \(0\), which is transient.

To prove it’s transient, we can use a conditioning on the first step argument to get \(m_0 = h_{10}\), and \[ h_{i\,0} = \tfrac23 h_{i+1\,0} + \tfrac23 h_{i-1,\,0} . \] The general solution is \[ h_{i0} = A + B\left(\tfrac12\right)^i , \] since \(\rho = \frac13 / \frac23 = \frac12\). The initial condition \(h_{00} = 1\) gives \(A + B = 1\), so \[ h_{i0} = 1 - B\left(1 - \left(\tfrac12\right)^i\right) , \] and non-negative minimlality requires \(B = 1\). Hence \[ h_{i0} = \left(\tfrac12\right)^i , \] and \(m_0 = h_{10} = \frac12 < 1\), as required.

6. “Every Markov chain on a finite state space has at least one stationary distribution.” Explain carefully why this is true. You may use facts from the notes or previous example sheets, provided that you state them clearly.

Solution. In Problem Sheet 4, Question 3, we showed that every finite-state Markov chain has a closed communicating class. In lectures, we showed the finite closed communicating classes are positive recurrent. If we look at the Markov chain restricted to just such a positive recurrent and closed class, then that restricted Markov chain is irreducible and positive recurrent, so it has a stationary distribution \(\boldsymbol\pi\). Since the class is closed, we have a stationary distribution that is \(\boldsymbol\pi\) on the given closed class and \(0\) elsewhere.