Problem sheet 6
You should attempt all these questions and write up your solutions in advance of your workshop in week 7 (Monday 8 or Tuesday 9 March) where the answers will be discussed.
Remember that the mid-semester survey is still open.
1. Consider a Markov chain \((X_n)\) with state space \(\mathcal S =\{1,2,3\}\) and transition matrix \[ \mathsf P = \begin{pmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{pmatrix}. \]
(a) Draw a transition diagram for this Markov chain. Is it irreducible? Is each state periodic or aperiodic?
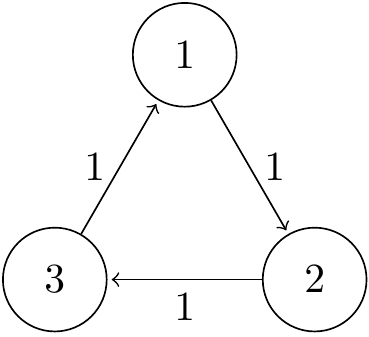
Figure 12.1: Transition diagram for Question 1.
The Markov chain is irreducible, since we have \(1 \to 2 \to 3 \to 1\). Since we continually cycle around the triangle, it’s clear that the period is \(d = 3\).
(b) What is \(m_i\), the return probability, for each state? What is \(\mu_i\), the expected return time for each state.
Solution. Again, since we continually cycle around the triangle, we always return in \(3\) steps, so \(m_i = 1\) and \(\mu_i =3\) for all \(i\).
(c) By solving \(\boldsymbol \pi = \boldsymbol\pi \mathsf P\), find the stationary distribution. Use this to confirm the values of \(\mu_i\).
Solution. The equations give \(\pi_1 = \pi_3\), \(\pi_2 = \pi_1\) and \(\pi_3 = \pi_2\), meaning they’re all equal. The normalising condition gives \(\boldsymbol\pi = (\frac13, \frac13, \frac13)\). The expected return times are \(\mu_i = 1/\pi_i = 3\), as predicted.
(d) For what initial distributions \(\boldsymbol\lambda\) do the limits \(\lim_{n \to \infty} \mathbb P(X_n = i)\) exist?
Solution. For a given initial condition \((\lambda_1, \lambda_2, \lambda_3)\) it’s clear we cycle through the initial condition, \((\lambda_2, \lambda_3, \lambda_1)\), and \((\lambda_3, \lambda_1, \lambda_2)\). Hence the limits only exist if \(\lambda_1 = \lambda_2 = \lambda_3 = \frac13\).
(e) What is the long-run proportion of time spent in each state?
Solution. Since the Markov chain is irreducible and positive recurrent (like every finite irreducible chain), the ergodic theorem tells us that the long-run proportion of time spent in each state \(i\) is \(\pi_i = \frac13\).
2. Every person has two chromosomes; each chromosome is a copy of a chromosome from one of the person’s parents. There are two types of chromosome, which are conventionally labelled X and Y. A child born with a Y chromosome is male, while a child with two X chromosomes is female.
Haemophilia is a blood-clotting disorder caused by a defective X chromosome (we will label this as \(\text X^*\)). Females with the defective chromosome (\(\text X^*\text X\)) will not typically show symptoms of the disease but can pass it on to children – they are “carriers”. Males with the defective chromosome (\(\text X^* \text Y\)) have the disease and its symptoms.
A medical statistician is studying the progress of the disease through first-born children, starting with a female carrier. The statistician makes the following assumptions: First, each parent has an equal probability of passing either of their chromosomes to their children. Second, the partner of each person in the study does not have a defective X chromosome. Third, no new genetic disorders occur.
(a) Show that we can use a Markov chain to model the progress of the disease under the above assumptions. What is the state space? Draw a transition diagram.
Solution. Consider a stochastic process on the state space \(\mathcal S = \{\text{F}, \text{M}, \text{m}, \text{f}\}\), where F means the first-born child is a female carrier, M means the child is a male haemophiliac, f means the child is a female non-carrier, and m means the child is a male without the disease. (This is not the only way to set up the Markov chain.) If we let \((X_n)\) be the status of the first-born child at the \(n\)th generation, then it is clear that \(X_{n+1}\), the status of the \((n+1)\)st individual, will depend on the status of their parent \(X_n\), but, given that, will not depend further on the history of the process. So we have the Markov property.
The transition probabilities are: From a female carrier, \(p_{\mathrm{FF}} = \frac14\) or \(p_{\mathrm{FM}} = \frac14\) if she passes on the \(\text X^*\), or \(p_{\mathrm{Ff}} = p_{\mathrm{Fm}} = \frac14\) if not. From a male haemophiliac, \(p_{\mathrm{MF}} = \frac12\) if he passes on the \(\text X^*\), or \(p_{\mathrm{Mm}} = \frac12\) if not. From those without the \(\text X^*\), we have \(p_{\mathrm{ff}} = p_{\mathrm{fm}} = p_{\mathrm{mf}} =p_{\mathrm{mm}} = \frac12\).
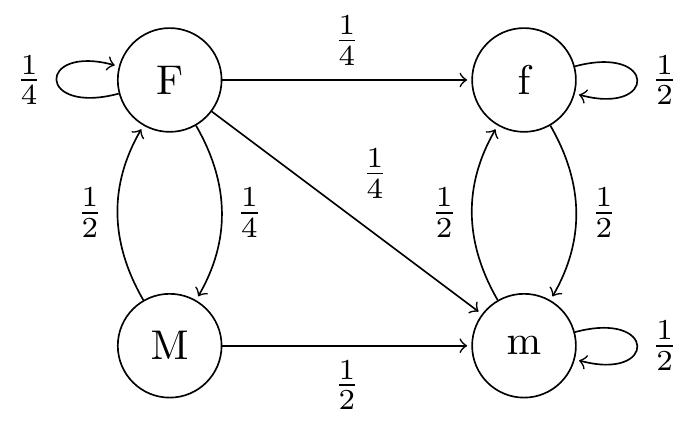
Figure 12.2: Transition diagram for Question 2.
(b) What are the communicating classes in the chain? Is each class positive recurrent, null recurrent, or transient?
Solution. Note we can move from F or M to f or m but not back again. So the class \(\{\text F, \text M\}\) is non-closed and thus transient, while the class \(\{\text f, \text m\}\) is closed and thus positive recurrent.
(c) Calculate a stationary distribution. Is this the only stationary distribution?
Solution. We have a stationary distribution is \(\pi_{\mathrm M} = \pi_{\mathrm{F}} = 0\), \(\pi_{\mathrm m} = \pi_{\mathrm f} = \frac12\). One way to see this is to solve \(\boldsymbol\pi = \boldsymbol\pi\mathsf P\). Another way is the following: Since F and M are transient we must have \(\pi_{\mathrm M} = \pi_{\mathrm{F}} = 0\). But, within the recurrent class, m and f are symmetrical, so we must have \(\pi_{\mathrm m} = \pi_{\mathrm f}\). The result follows.
Since there is exactly one positive recurrent class, the stationary distribution is unique.
(d) Under this model, what is the limiting probability that, in many generations’ time, a child has haemophilia?
Solution. Since M and F are transient states, we have \(\lim \mathbb P(X_n = \mathrm F) = \lim \mathbb P(X_n = \mathrm M) = 0\), so the limiting probability is \(0\).
3. An airline operates a frequent flyer scheme with four classes of membership; Ordinary, Bronze, Silver and Gold. Scheme members get benefits according to their membership class. Changing membership class operates as follows:
- If a member books two or more flights in a given year, they are moved up a class of membership for the next year (or remain at Gold).
- If a member books a single flight, they remain in their current class in the following year.
- If a member books no flights, they move down a class (or remain at Ordinary).
The airline’s research has shown that in a given year 40% of members book no flights, 40% book exactly one flight and the remaining 20% book two or more flights, independent of their history. Moreover, the cost of running the scheme per member is estimated as £0 for Ordinary members, £10 for Bronze members, £20 for Silver members, and £30 for Gold members.
(a) Show that this system can be modelled using a Markov chain. Write down the transition probabilities and draw a transition diagram.
Solution. We write \(\mathcal S = \{\text{O},\text{B},\text{S},\text{G}\}\) for the set of states, and let \(X_n\) be the membership level in year \(n\). Next year’s membership level depends on this year’s, but not, given this year’s, on the previous history, so we have the Markov property.
With probability \(40\%\), a member books no flights, giving \[ p_{\mathrm{BO}} = p_{\mathrm{SB}} = p_{\mathrm{GG}} = 0.4 . \] With probability \(40\%\), a member books one flights, giving \[ p_{\mathrm{BB}} = p_{\mathrm{SS}} = 0.4 \] and \(p_{\mathrm{OO}} = 0.4+0.4 = 0.8\). With probability \(20\%\), a member books two or more flights, giving \[ p_{\mathrm{OB}} = p_{\mathrm{BS}} = p_{\mathrm{SG}} = 0.2 \] and \(p_{\mathrm{GG}} = 0.4+0.2 = 0.6\).
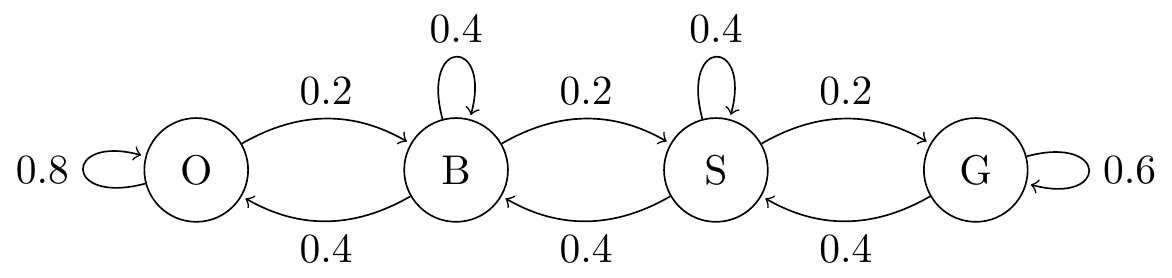
Figure 12.3: Transition diagram for Question 3.
(b) Explain why a unique stationary distribution exists and calculate it.
Solution. The Markov chain is irreducible and positive recurrent, so has a unique stationary distribution.
The equations from \(\boldsymbol\pi = \boldsymbol\pi \mathsf P\) are \[\begin{align} \pi_{\mathrm O} &= 0.8 \pi_{\mathrm O} + 0.4 \pi_{\mathrm B } \\ \pi_{\mathrm B} &= 0.2\pi_{\mathrm O} + 0.4\pi_{\mathrm B} + 0.4\pi_{\mathrm S} \\ \pi_{\mathrm S} &= \phantom{0.2 \pi_{\mathrm S} +} 0.2 \pi_{\mathrm B} + 0.4 \pi_{\mathrm S} + 0.4 \pi_{\mathrm G} \\ \pi_{\mathrm G} &= \phantom{0.2 \pi_{\mathrm S} + 0.2 \pi_{\mathrm B} +} 0.2 \pi_{\mathrm S} + 0.6 \pi_{\mathrm G} . \end{align}\] We will choose \(\pi_{\mathrm B}\) as the working variable and discard the last equation. Rearranging the other three equations gives \[\begin{align*} \pi_{\mathrm O} \phantom{{}+ 2\pi_{\mathrm S} - 2\pi_{\mathrm G}} &= 2\pi_{\mathrm B} \\ \pi_{\mathrm O} + 2\pi_{\mathrm S} \phantom{{}- 2\pi_{\mathrm G}} &= 3\pi_{\mathrm B} \\ 3\pi_{\mathrm S} - 2\pi_{\mathrm G} &= \pi_{\mathrm B} \end{align*}\] Substituting the first of these into the second and rearranging gives \(\pi_{\mathrm S} = \frac12 \pi_{\mathrm B}\). Substituting this into the third and rearranging gives \(\pi_{\mathrm S} = \frac14 \pi_{\mathrm B}\)
The normalising condition is \[ \pi_{\mathrm O} + \pi_{\mathrm B} + \pi_{\mathrm S} + \pi_{\mathrm G} = \left(2 + 1 + \tfrac12 + \tfrac14 \right)\pi_{\mathrm B} = \tfrac{15}{4} \pi_{\mathrm B} = 1 . \] Hence \(\pi_{\mathrm B} = \frac{4}{15}\). Back-solving, we get the solution \[ \left(\pi_{\mathrm O},\pi_{\mathrm B},\pi_{\mathrm S},\pi_{\mathrm G}\right) = \left(\tfrac8{15},\tfrac{4}{15},\tfrac{2}{15},\tfrac{1}{15} \right) . \]
(c) The airline makes a profit of £10 per passenger per flight, before the cost of the frequent flyer scheme. In the long run, does the airline expect to remain in profit after the cost of the scheme?
Solution. By the ergodic theorem, the long run time spent in state \(x\) is \(\pi_x\). So the long-run cost per member is \[ 0\pi_{\mathrm O} + 10\pi_{\mathrm B} + 20 \pi_{\mathrm S} + 30\pi_{\mathrm G} = 0 \cdot\tfrac8{15} + 10\cdot\tfrac{4}{15} + 20\cdot\tfrac{2}{15} + 30 \cdot \tfrac{1}{15} = \tfrac{110}{15} = \tfrac{22}{3} , \] for a cost of 7.33. The average number of flights taken per member is at least \[ 0.4\times 0 + 0.4 \times 1 + 0.2\times 2 = 0.8 , \] for a profit of at least \(10\times0.8 = \text{\pounds}8\). (“At least” because the probability \(0.2\) refers to “two or more” flights.) Since \(8 >7.33\), the airline will make a profit in the long run.
4. We have \(N\) balls, each of which is placed into one of two urns. At each time step, a ball is chosen uniformly at random and moved to the other urn.
(a) Show that the stationary probability the first urn contains \(i\) balls is \[ \frac{1}{2^N} \binom{N}{i} . \]
Solution. One way to solve this is to let \(X_n\) be the number of balls in the first urn after having moved \(n\) balls. This has transition probabilities \[ p_{i,i+1} = 1 - \frac{i}{N} \qquad p_{i,i-1} = \frac{i}{N} . \] The equations for the stationary distribution are \[ \pi_i = \left(1 - \frac{i-1}{N}\right)\pi_{i-1} + \frac{i+1}N \pi_{i+1} . \] One can check that \(\pi_i = C \binom{N}{i}\) satisfies this for any constant \(C\) by using the combinatorial identities \[\begin{align*} \left(1 - \frac{i-1}{N}\right)\binom{N}{i-1} &= \binom{N-1}{i-1} \\ \frac{i+1}N \binom{N}{i+1} &= \binom{N-1}{i} \\ \binom{N-1}{i-1} + \binom{N-1}{i} &= \binom Ni , \end{align*}\] and check that the normalising condition demands \(C = 1/2^N\) because of \[ \sum_{i=0}^N \binom Ni = 2^N . \]
The following is perhaps a better way. Let \(Y_n^j = 1\) denote that ball \(j\) is in the first urn at time \(n\), and \(Y_n^j = 2\) denote that it is in the second urn. Let \(\mathbf Y_n = (Y_n^1, Y_n^2, \dots, Y_n^N)\). Then \((\mathbf Y_n)\) is a Markov chain on the state space \(\mathcal S = \{1,2\}^N\). The transition probabilities are that \(p_{\mathbf{yz}} = 1/N\) for any \(\mathbf y, \mathbf z \in \mathcal S\) that differ in exactly one of the \(N\) coordinates. Because of the symmetry, it’s clear that we have a stationary distribution \(\boldsymbol\phi = (\phi_{\mathbf y})\) where \(\phi_{\mathbf y} = 1/|\mathcal S| = 1/2^N\) for all \(\mathbf y \in \mathcal S\). Since the Markov chain is irreducible and positive recurrent, this is the only stationary distribution. Hence the stationary probability the first urn contains \(i\) balls is \[ \sum_{\mathbf y \in \mathcal S(i)} \phi_{\mathbf y} = \big|\mathcal S(i)\big|\, \frac{1}{2^N} = \binom{N}{i} \frac 1{2^N} , \] where \(\mathcal S(i)\) is the set of \(\mathbf y \in \mathcal S\) consisting of \(i\) \(1\)s and \(N-i\) \(2\)s.
(b) Is this an equilibrium distribution?
Solution. No. The number of balls in the left-hand urn switches between odd and even each turn, so the chain is periodic with period 2, and does not have an equilibrium distribution.
(c) In the long run, for what proportion of time are all of the balls in the same urn?
Solution. By the ergodic theorem, the long run proportion of time that all the balls are in the same urn is \[ \pi_0 + \pi_N = \phi_{(1,1,\dots,1)} + \phi_{(2,2,\dots,2)} = \frac{1}{2^N} + \frac{1}{2^N} = \frac{1}{2^{N-1}} . \]