Section 7 Class structure

Communicating classes and irreducibility
Period of a state (and class)

7.1 Communicating classes

If we have a large complicated Markov chain, it can be useful to split the state space up into smaller pieces that can be studied separately. The idea is that states \(i\) and \(j\) should definitely be in the same piece (or "class) if we can get from \(i\) to \(j\) and then back to \(i\) again after some number of steps.

Definition 7.1 Consider a Markov chain on a state space \(\mathcal S\) with transition matrix \(\mathsf P\). We say that state \(j\in\mathcal{S}\) is accessible from state \(i\in\mathcal{S}\) and write \(i \to j\) if, for some \(n\), \(p_{ij}(n)>0\).

If \(i \to j\) and \(j \to i\), we say that \(i\) communicates with \(j\) and write \(i \leftrightarrow j\).

Here, the condition \(p_{ij}(n)>0\) means that, starting from \(i\), there’s a positive chance that we’ll get to \(j\) at some point in the future – hence the term “accessible”.

Theorem 7.1 Consider a Markov chain on a state space \(\mathcal S\) with transition matrix \(\mathsf P\). Then the “communicates with” relation \(\leftrightarrow\) is an equivalence relation; that is, it has the following properties:

reflexive: \(i \leftrightarrow i\) for all \(i\);
symmetric: if \(i \leftrightarrow j\) then \(j \leftrightarrow i\);
transitive: if \(i \leftrightarrow j\) and \(j \leftrightarrow k\) then \(i \leftrightarrow k\).

Proof. Reflexivity: Clearly \(p_{ii}(0) = 1 > 0\), because in “zero steps” we stay where we are. So \(i \leftrightarrow i\) for all \(i\).

Symmetry: The definition of \(i \leftrightarrow j\) is symmetric under swapping \(i\) and \(j\).

Transitivity. If we can get from \(i\) to \(j\) and we can get from \(j\) to \(k\), then we can get from \(i\) to \(k\) by going via \(j\). We just need to write that out formally.

Since \(i \to j\), we have \(p_{ij}(n) > 0\) for some \(n\), and since \(j \to k\), we also have \(p_{jk}(m) > 0\) for some \(m\). Then, by the Chapman–Kolmogorov equations, we have \[ p_{ik}(n+m) = \sum_{l \in \mathcal S} p_{il}(n) p_{lk}(m) \geq p_{ij}(n) p_{jk}(m) > 0 , \] from just picking out the \(l=j\) term in the sum. So \(i \to k\) too.

The same argument with \(k\) and \(i\) swapped gives \(k \to i\) also, so \(i \leftrightarrow k\).

A fact you may remember about equivalence relations is that an equivalence relation, like \(\leftrightarrow\), partitions the space \(\mathcal S\) into equivalence classes. This means that each state \(i\) is in exactly one equivalence class, and that class is the set of states \(j\) such that \(i \leftrightarrow j\). In this context, we call these communicating classes.

Example 7.1 In the simple random walk, provided \(p\) is not 0 or 1, every state communicates with every other state, because from \(i\) when can get to \(j > i\) by going up \(j - i\) times, and we can get to \(j < i\) by going down \(i - j\) times. Therefore the whole state space \(\mathcal S = \mathbb Z\) is one communicating class.

Example 7.2 Consider the gambler’s ruin Markov chain on \(\{0,1,\dots,m\}\). There are three communicating classes. The ruin states \(\{0\}\) and \(\{m\}\) each don’t communicate with any other states, so each are a class by themselves. The remaining states \(\{1,2,\dots,m-1\}\) are all in the same class, like the simple random walk.

Example 7.3 Consider the following simple model for an epidemic. We have three states: healthy (H), sick (S), and dead (D). This transition matrix is \[ \mathsf P = \begin{pmatrix} p_{\mathrm{HH}} & p_{\mathrm{HS}} & 0 \\ p_{\mathrm{SH}} & p_{\mathrm{SS}} & p_{\mathrm{SD}} \\ 0 & 0 & 1 \end{pmatrix} , \] and the transition diagram is:

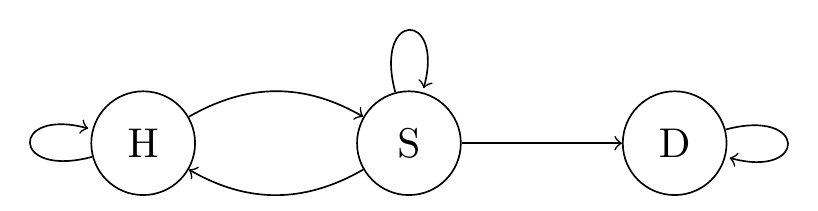
Figure 7.1: Transition diagram for the healthy–sick–dead chain.

Clearly H and S communicate with each other (you can become infected or recover), while D only communicates with itself (the dead do not recover). Hence, the state space \(\mathcal S = \{\mathrm{H},\mathrm{S},\mathrm{D}\}\) partitions into two communicating classes: \(\{\mathrm{H},\mathrm{S}\}\) and \(\{\mathrm{D}\}\).

A few more definitions that will be important later.

Definition 7.2 If the entire state space \(\mathcal S\) is one communicating class, we say that the Markov chain is irreducible.

We say that a communicating class is closed if no state outside the class is accessible from any state within the class. That is, class \(C \subset \mathcal S\) is closed if whenever there exist \(i \in C\) and \(j \in \mathcal S\) with \(i \to j\), then \(j \in C\) also. If a class is not closed, we say it is open.

If a state \(i\) is in a communicating class \(\{i\}\) by itself and that class is closed, then we say state \(i\) is absorbing.

In non-maths language:

An irreducible Markov chain can’t be broken down into smaller pieces.
Once you enter a closed class, you can’t leave that class.
Once you reach an absorbing state, you can’t leave that state.

How do these work for our earlier examples?

Example 7.4 Going back to the previous examples:

In the simple random walk, the whole state space is one communicating class which must therefore be closed. The Markov chain has only one class, so is irreducible.
In the gambler’s ruin, classes \(\{0\}\) and \(\{m\}\) are closed, because the Markov chain stays there forever, and because these closed classes consist of only one state each, \(0\) and \(m\) are absorbing states. The class \(\{1, 2, \dots, m-1\}\) is open, as we can escape the class by going to \(0\) or \(m\). The gambler’s ruin chain has multiple classes, so is not irreducible.
In the “healthy–sick–dead” chain, the class \(\{D\}\) is closed, so D is an absorbing state, while the class \(\{H, S\}\) is open, as one can leave it by dying. The Markov chain is not irreducible.

7.2 Periodicity

When we discussed the simple random walk, we noted that it alternates between even-numbered and odd-numbered states. This “periodic” behaviour is important to understand if we want to know which state we will be in at some point in the future.

The idea is this: List the number of steps for all possible paths starting and ending in the state. Then the period is the greatest common divisor (or “highest common factor”) of the integers in this list.

Definition 7.3 Consider a Markov chain with transition matrix \(\mathsf P\). We say that a state \(i\in\mathcal{S}\) has period \(d_i\), where \[ d_i=\text{gcd}\big\{n\in\{1,2,\dots,\} : p_{ii}(n) > 0\big\} , \] where gcd denotes the greatest common divisor.

If \(d_i>1\), then the state \(i\) is called periodic; if \(d_i = 1\), then \(i\) is called aperiodic.

Example 7.5 Consider the simple random walk with \(p \neq 0,1\). We have \(p_{ii}(n) = 0\) for odd \(n\), since we swap from odd to even each step. But \(p_{ii}(2) = 2pq > 0\). Therefore, all states are periodic with period \(\text{gcd}\{2,4,6,\dots\} = 2\).

Example 7.6 For the gambler’s ruin, states \(0\) and \(m\) are aperiodic (have period \(1\)), since they are absorbing states. The remaining states states \(1,2,\dots,m-1\) are periodic with period \(2\), because we swap between odd and even states, as in the simple random walk.

Example 7.7 Consider the Markov chain with transition diagram as shown:

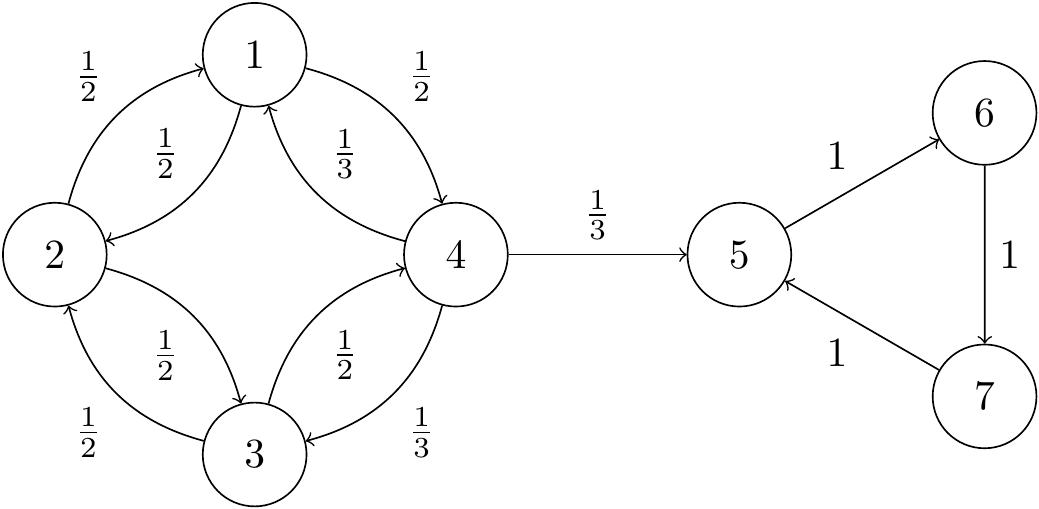
Figure 7.2: Transition diagram for an aperiodic irreducible Markov chain.

Importantly, we can’t return from the triangle side back to the circle side. We thus see there are two communicating classes: \(\{1,2,3,4\}\), which is open, and \(\{5,6,7\}\), which is closed. The Markov chain is not irreducible, and there are no absorbing states.

The circle side swaps between odd and even states (until exiting from \(4\) to \(5\)), so states \(1\),\(2\), \(3\) and \(4\) all have period \(2\). The triangle side cycles around with certainty, meaning that states \(5\), \(6\), and \(7\) all have period \(3\).

You may have noticed in these examples that, within a communicating class, every state has the same period. In fact, it’s always the case that states in the same class have the same period.

Theorem 7.2 All states in a communicating class have the same period.

Formally: Consider a Markov chain on a state space \(\mathcal S\) with transition matrix \(\mathsf P\). If \(i,j\in\mathcal S\) are such that \(i \leftrightarrow j\), then \(d_i = d_j\).

In particular, in an irreducible Markov chain, all states have the same period \(d\). We say that an irreducible Markov chain is periodic if \(d>1\) and aperiodic if \(d=1\).

Proof. Let \(i,j\) be such that \(i \leftrightarrow j\). We want to show that \(d_i = d_j\). First we’ll show that \(d_i \leq d_j\), and then we’ll show that \(d_j \leq d_i\), and thus conclude that they’re equal.

Since \(i\leftrightarrow j\), there exist \(n,m\) such that \(p_{ij}(n)>0\) and \(p_{ji}(m)>0\). Then, by the Chapman–Kolmogorov equations, \[ p_{ii}(n+m) = \sum_{k \in \mathcal S} p_{ik}(n) p_{ki}(m) \geq p_{ij}(n) p_{ji}(m) > 0 . \] So \(d_i\) divides \(n+m\).

Let \(r\) be such that \(p_{jj}(r)>0\). Then, by the same Chapman–Kolmogorov argument, \[ p_{ii}(n+m+r)\geq p_{ij}(n) p_{jj}(r) p_{ji}(m) > 0, \] because we can get from \(i\) to \(i\) by going \(i \to j \to j \to i\). Hence \(d_i\) divides \(n+m+r\).

But if \(d_i\) divides both \(n+m\) and \(n+m+r\), it must be that \(d_i\) divides \(r\) also. So whenever \(p_{jj}(r)>0\), we have that \(d_i\) divides \(r\). Since \(d_i\) is a common divisor of all the \(r\)s with \(p_{jj}(r)>0\), it can’t be any bigger that the greatest common divisor of all those \(r\)s. But that greatest common divisor is by definition \(d_j\), the period of \(j\). So \(d_i \leq d_j\).

Repeating the same argument but with \(i\) and \(j\) swapped over, we get \(d_j\leq d_i\) too, and we’re done.

In the next section, we look at two problems to do with “hitting times”: What is the probability we reach a certain state, and how long on average does it take us to get there?